ficha 5

Exercicio 1

Relembrem a definição de “ap” e de “swap”:

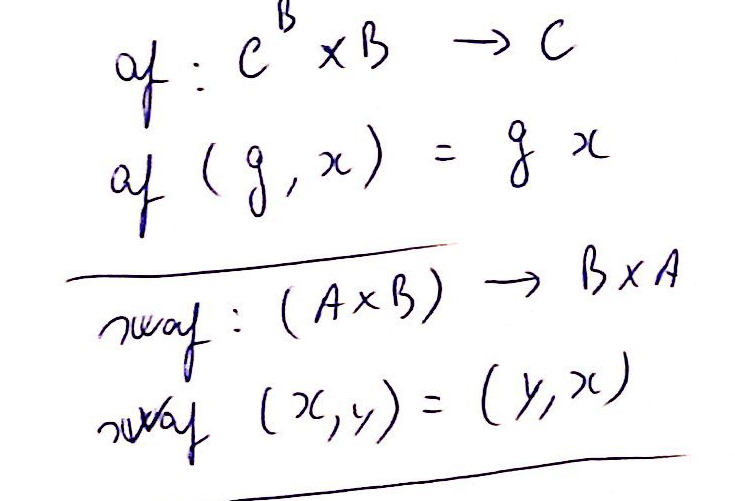
Ou se quiserem em Haskell:

ap:: ((b->c), b) -> c  
ap (f,x) = f xswap:: (a,b) -> (b,a)  
swap (x,y) = (y,x)

Também será útil relembrar:

uncurry :: (a -> b -> c) -> (a,b) -> c  
uncurry f (x,y) = f x ycurry :: ((a,b) -> c) -> a -> b -> c  
curry f x y = f(x,y)

Então

flip f = curry ((uncurry f).swap)  
<=> {33 } 
ap.(flip f x id) = (uncurry f).swap 
<=> { 69}  
ap.(flip f x id) (x,y) = (uncurry f).swap (x,y) 
<=> { 70} 
ap ((flip f x id) (x,y)) = (uncurry f) (swap (x,y))  
<=> { }  
ap (flip f x, id y) =uncurry f (y,x)  
<=> { } 
flip f x y = f y x

Exercicio 2

Relembrar in=[zero,succ] sendozero: 1 -> Nat
zero x = 0 (note que zero é equivalente à função constante (const 0)) succ: Nat -> Nat succ x = x+1

Relembrem o diagrama do combinador catamorfismo de naturais e a respectiva propriedade universal: k=(|g|) <=> k.in=g.(id+k) Comecemos por desenhar o diagrama do catamorfismo de naturais para for b i

Obtemos então:

for b i = (| [(const i), b] |)

E desenvolvendo

for b i = (| [(const i), b] |)
<=>{ 43 }
(for b i) . in = [(const i), b] . (id + (for b i))
<=> { def. in, 22, 1 }
(for b i) . [zero,succ] = [(const i).id, b.(for b i)]
<=> {20}
[(for b i).zero, (for b i).succ] = [(const i).id, b.(for b i)]
<=> {27}
(for b i).zero = (const i)
(for b i).succ = b.(for b i)
<=> 69, 70
(for b i) (zero ()) = (const i) ()
(for b i) (succ n) = b ((for b i) n)
<=> 72, def. succ, def. zero
for b i 0 = i
for b i (n+1) = b (for b i n)

Exercicio 3

Vamos então derivar a versão point wise a partir de

(a+) = (| [(const a), succ] |)

Temos então

(a+) = (| [(const a), succ] |)  
<=>{ 43 }  
(a+) . in = [(const a), succ] . (id + (a+))  
<=> { def. in, 22, 1 }  
(a+) . [zero,succ] = [(const a).id, succ.(a+)]  
<=> {20}  
[(a+).zero, (a+).succ] = [(const a).id, succ.(a+)]  
<=> {27}  
(a+).zero = (const a)  
(a+).succ = succ.(a+)  
<=>{ 69, 70}  
(a+) (zero ()) = (const a) ()  
(a+) (succ n) = succ ((a+) n)  
<=> {72, def. succ, def. zero}  
a+ 0 = a  
a+ (n+1) = (a+n) + 1

Exercicio 4

Vou começar por alterar o nome da função para (a#) para facilitar a escrita.
Desenhem o diagrama do catamorfismo de naturais para (a#)=(| [(const k),g] |) 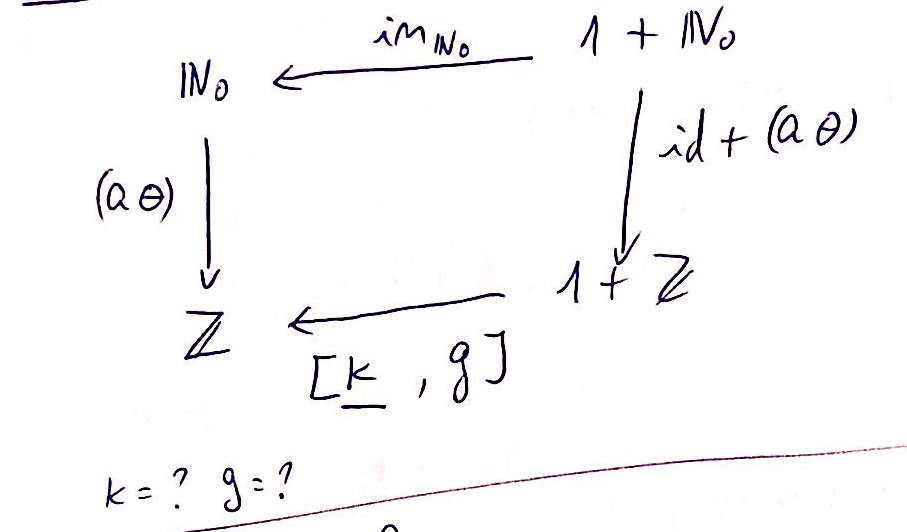Reparem que para (a#) 0 temos: 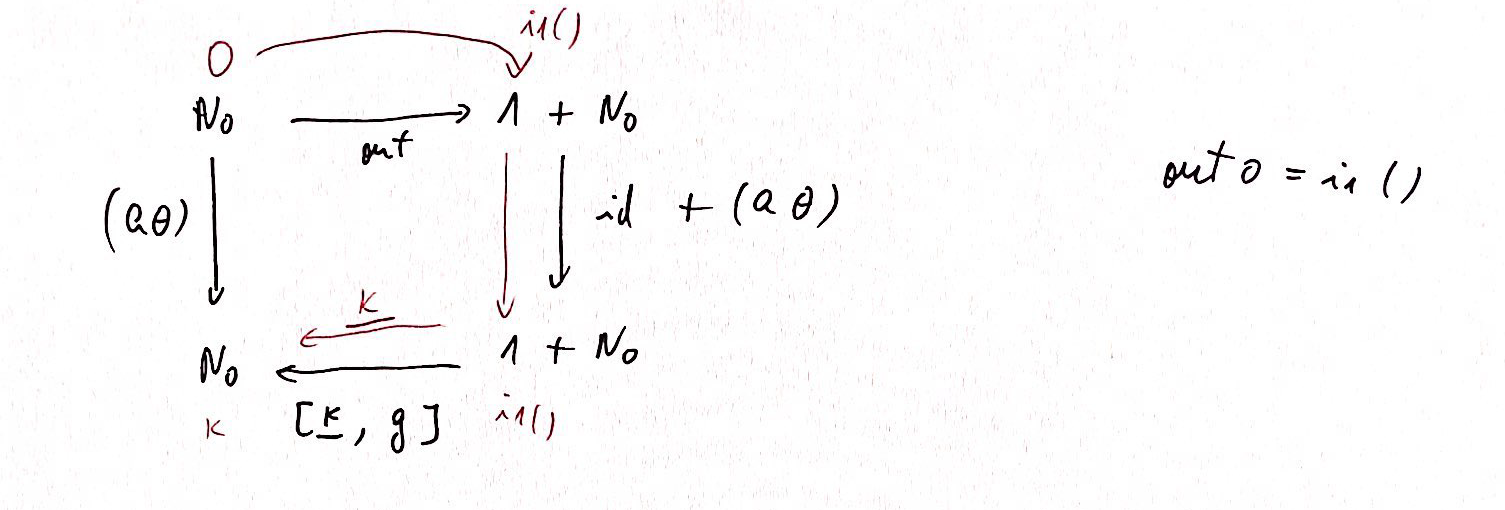e para (a#) n temos: 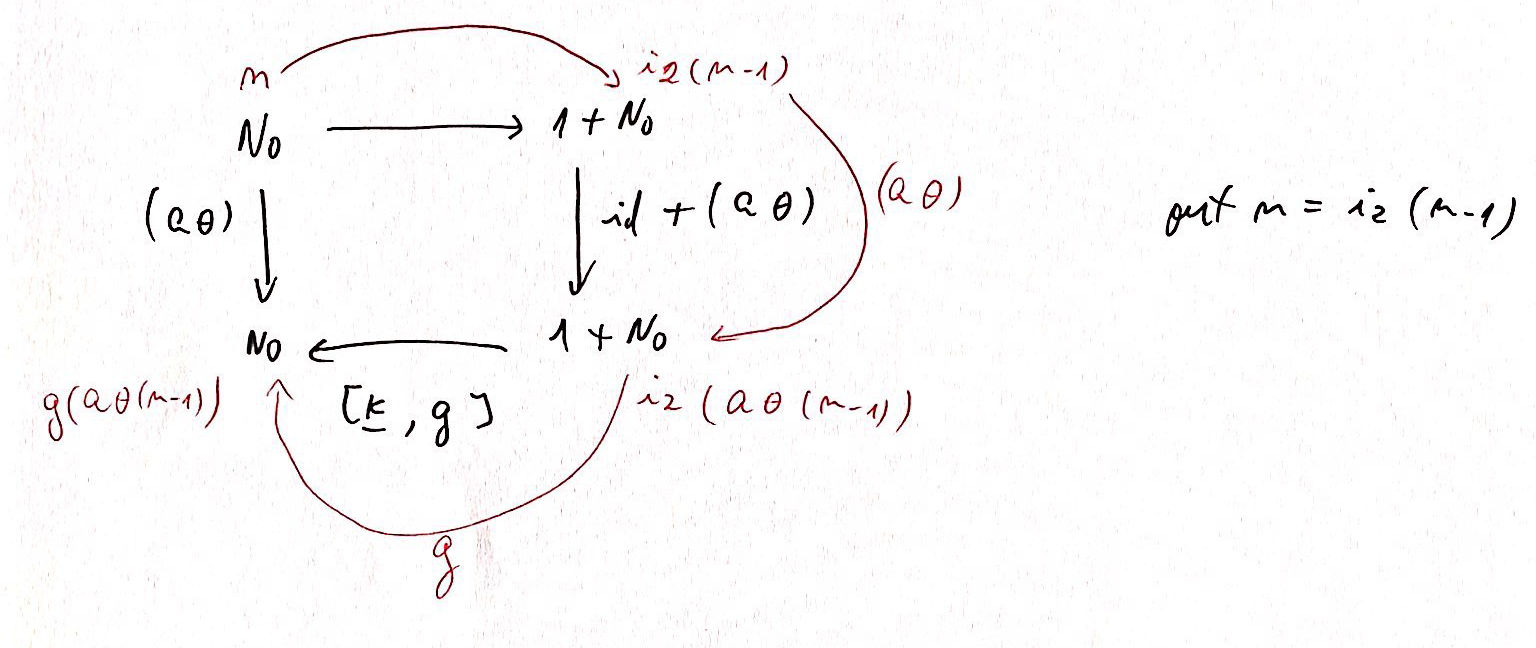Ficamos, então

a # 0 = a  
a # (n+1) = (a # n) - 1
<=> {def. pred, def succ, def. zero, 72}
a # (zero ()) = (const a) ()  
a # (succ n) = pred (a # n)
<=>{ 69, 70}(a#).zero = (const a)  
(a #).succ = pred.(a #)
<=> {27,1}
[(a#).zero, (a#).succ] = [(const a).id, pred.(a#)]
<=> {20, 22}
(a#) . [zero,succ]= [(const a), pred] . (id + (a#))
<=> def in, F f=id+f
(a#).in = [(const a), pred] . F (a#)
<=>{ 43 }
(a#) = (| [(const a), pred] |)

k=a e g=pred

Exercicio 5

Relembre a propriedade cancelamento-cata (44) para naturais: (|g|) . in = g . (id + (|g|))

Verifique que se pode reescrever como: (|g|)= g . (id + (|g|)).out

Na aula anterior calculamos o out para naturais:

outNat 0 = i1 ()  
outNat (n+1) = i2 nou de forma equivalente:outNat 0 = i1 ()  
outNat n = i2 (n-1)

Use agora os combinadores estudados e codificados em Cp.hs para codificar (|g|)= g . (id + (|g|)).out

funcNat f = id -|- f

é só usar o combinador -

-

Vamos agora a (

g

)cataNat = cataNat g = g . funcNat (cataNat g) . outNat

Codifique agora: for b i =

Temos for b i=(| [(const i), b] |). Logo:

for b i = cataNat (either (const i) b)

Está agora em condições de codificar:

f = p2 . aux
where aux = for (split (succ . p1) mul) (1,1)
mul (x,y) = x*y

Vamos analisar com um diagrama qual o resultado de aux 0 ?

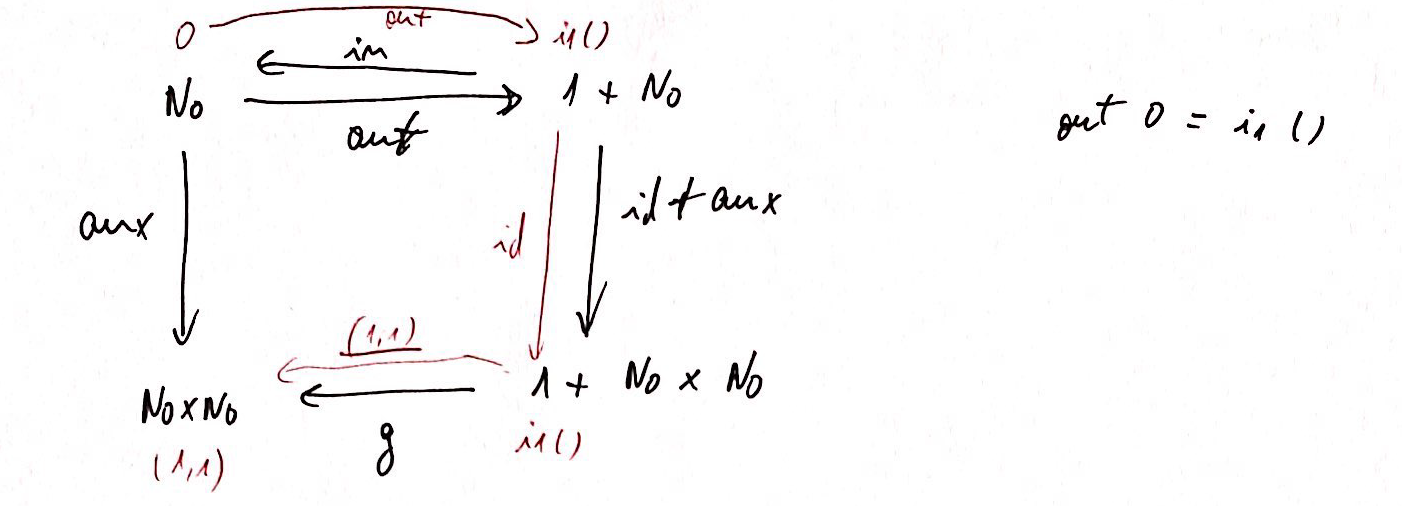
e aux 1

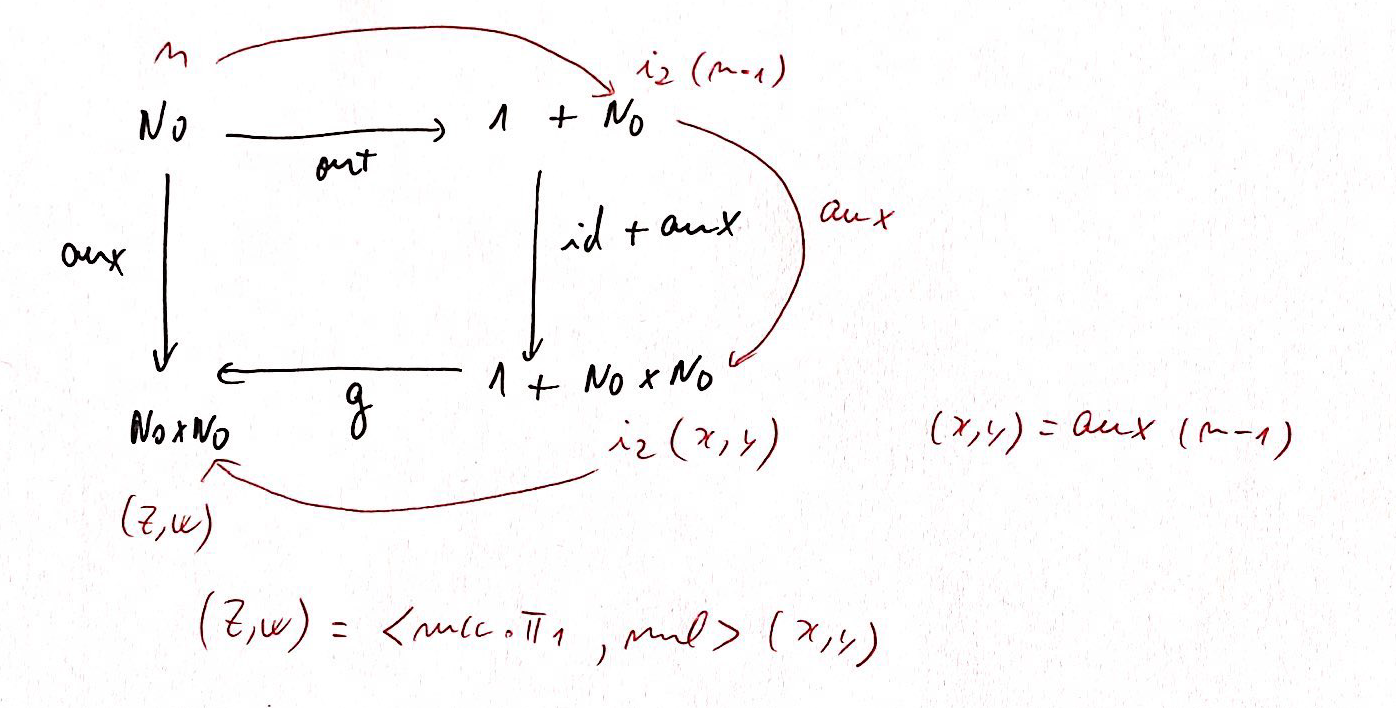
f0=1 f1=1 f2=2 f3=6 …

Notas

Tirando partidos dos catamorfismos, iremos ver como lidar com recursividade de forma muito mais estruturada e compacta em relação ao que vocês tem visto na programação. Por exemplo, iremos ver que a função,

length : [a] -> Int
length [] = 0
length (x:xs) = 1 + (len xs)

se reduz a,

length :: [a] -> Int
length = cataList (either (const 0) ((1+) . p2))

e que a função que agrega listas,

flatt :: [[a]] -> [a]
flatt [] = []
flatt (x:xs) = x ++ (flatt xs)

se reduz a,

flatt :: [[a]] -> [a]
flatt = cataList (either (const []) (uncurry (++)))

E que a função que soma todos os valores em folhas de árvores,

summ :: LTree Int -> Int
summ (Leaf x) = x
summ (Fork(x,y)) = (summ x) + (summ y)

se reduz a,

summ :: LTree Int -> Int
summ = cataLTree (either id (uncurry (+)))